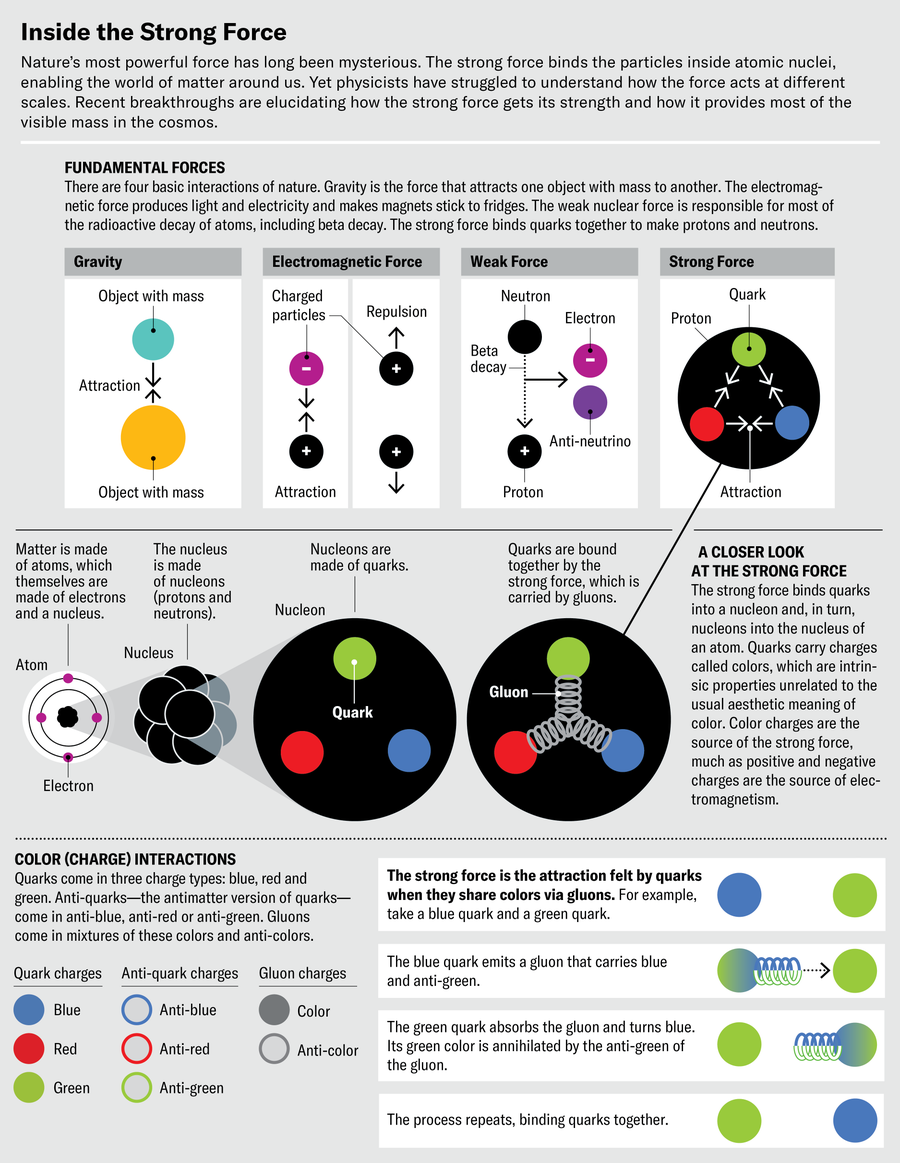
The strongest force in the universe is called, aptly, the strong force. We never get to witness its fearsome power because it works only across subatomic distances, where it binds quarks together inside protons and neutrons and joins those nucleons into atomic nuclei. Of the four basic forces of nature, the strong force is by far the most potent—it’s 100 trillion trillion trillion times stronger than the force of gravity. It’s also the most mysterious.
Despite knowing roughly how it compares with the other forces, scientists don’t know precisely how strong the strong force is. The other three forces—gravity, the electromagnetic force and the weak nuclear force (responsible for some radioactivity)—are much better measured. The strength of electromagnetism, for example, denoted by its “coupling constant,” has been measured with the same precision as the distance between New York and Los Angeles, to within a few hair breadths. Yet the strong force’s coupling constant, called αs (“alpha s”), is by far the least understood of these quantities. The precision of the best measurements of αs is 100 million times worse than that of the electromagnetic measurement.
Even this level of (un)certainty is known only in the simplest domain of the strong force theory, at very high energies involved only in some of the rarest and most extreme events in nature. At the lower energies relevant to the world around us, the strong force earns its name by becoming truly intense, and concrete information on αs in this range is scarce. Until recently, no one had made any experimental measurements of αs at this scale. Theoretical predictions for its value were unhelpful, covering the entire span from zero to infinity.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Jen Christiansen
The strong force’s might makes it difficult to study in lots of ways. The theory describing how it works, called quantum chromodynamics, is so complicated we can’t use it to make direct calculations or precise predictions. One of the reasons for this complexity is that the carrier of the strong force—a particle called the gluon—interacts with itself. Electromagnetism, in comparison, is simple because its carrier, the photon, is chargeless. But the gluon carries the strong force’s version of charge, called color, and its self-interactions quickly get out of hand. So despite its importance to nuclear physics and building the material world, the strong force is not unconditionally loved by researchers. Instead many look at the domain where the strong force is truly strong as a “Terra Damnata,” a realm to avoid at all costs.
Yet understanding the strong force is essential for explaining the complexity of the matter around us. In fact, the strong force accounts for the origin of around 99 percent of the mass in the visible universe. (The remaining 1 percent comes from the Higgs boson.) And now, after half a century of effort, scientists have finally begun revealing some of the strong force’s secrets. One of us (Deur) recently made the first measurements of how αs changes within Terra Damnata, and two of us (Brodsky and Roberts) independently developed new theoretical predictions that explained the data. Terra Damnata is looking more welcoming than ever before. And now that we can explore this terrain, we stand to learn much more. We at last have the ability to analytically calculate aspects of quantum chromodynamics from first principles. Furthermore, exploring this range of the strong force could help us understand proposed unifying theories of the universe, as well as the question of how many dimensions exist in space and time.

Magnets direct particles through the Continuous Electron Beam Accelerator Facility (CEBAF) at the Thomas Jefferson National Accelerator Facility.
Courtesy of Jefferson Lab
If αs is a constant, how can it change? The answer has to do with the concept of quantum loops, also known as vacuum polarization. Quantum theory revealed that the “vacuum” of space is actually full of tiny particles that are constantly appearing and disappearing in fluctuating clouds. Interactions with these virtual particles can cause a force to depart from its classical behavior because of what’s called a quantum loop. When the notion was first introduced, quantum loops were an unpleasant surprise because they predict infinite quantities—a clear sign that something is wrong. But eventually physicists figured out how to tame these infinities and absorb all the corrections from quantum loops into the equation describing the carrier of the force. Thus, in quantum chromodynamics (QCD), quantum loop corrections affect the gluon’s behavior and determine how much αs changes with the distance between quarks. With this new distance dependence from quantum loops lodged within the coupling constant, these quantities lost their constancy. So we’ll just call them “couplings” from now on.
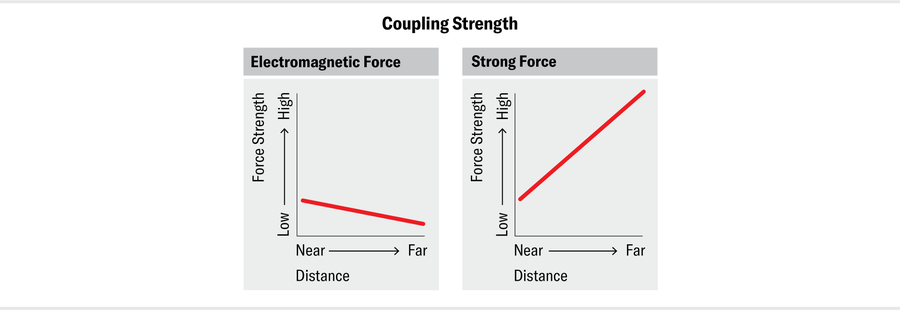
For most of the forces, the couplings change slowly with distance. For instance, from the tiniest scales ever probed by humans to everyday scales, αem, the electromagnetic coupling, decreases only by about 10 percent of its value. For the strong coupling, αs, however, the change is huge: even within the domain where physicists are comfortable calculating αs (that is, far from Terra Damnata), its value changes by several orders of magnitude. Another difference, far more important, is that the electromagnetic coupling decreases as the distance grows. For the strong force, however, αs increases with distance. If you try to pull two quarks within a proton apart from each other, the attraction between them becomes stronger. In fact, it grows so powerfully that it’s essentially impossible to pry quarks away from each other—the strong force keeps them “confined,” and you can never find a single quark by itself. The same rule applies to interactions between quarks and gluons and between gluons and gluons. The flip side is that these interactions are weak at short distances: the closer you zoom in on a quark, the more loosely it’s bound. The smallness of αs at small distances is called asymptotic freedom, and its discovery in the 1970s eventually won its pioneers the 2004 Nobel Prize in Physics.
Jen Christiansen
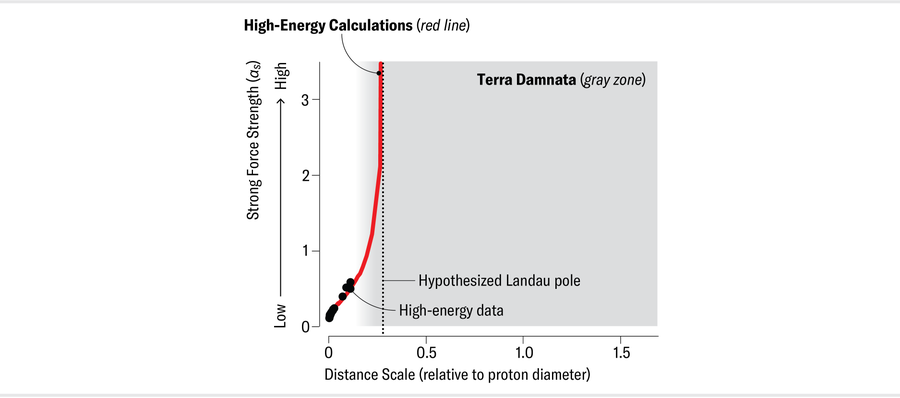
At short distances, where αs is small, physicists can perform calculations using the same methods that we use for the electromagnetic and weak forces. But these methods don’t work for QCD at longer distances—say, the size of a proton. This length is, by everyday standards, still very small (the proton, being one-50,000th the size of an atom, has a radius of roughly a millionth of a billionth of a meter). Yet it represents an expanse in particle physics. The problem is that αs grows too quickly. Before we can reach a fermi, αs becomes too big for the standard calculation method to be applicable. This is why the (not even very) long-distance domain became Terra Damnata.
Jen Christiansen
With the usual calculation method unavailable, physicists tried other strategies, but they were either less well tested or imprecise and predicted a long-distance limit for αs that could lie anywhere between zero and infinity. The usual short-distance calculation method predicts an infinite value of αs at long range. But this infinity, referred to as the Landau pole after physicist Lev Landau, reveals only that the computational method has failed rather than telling us about the strong force. It was crucial to determine what αs does at a distance.
A breakthrough has finally emerged from a wide-ranging effort by many physicists. The tale unfolds in three stages, and one of us played a part in each.
The first step was fortuitous. In the late 1990s Deur was a Ph.D. student taking data at the Thomas Jefferson National Accelerator Facility (Jefferson Lab) in Virginia, which houses a particle accelerator. His measurements spanned the transition between short distances and Terra Damnata. At the time, he knew of the Landau pole but not that it was bogus. He was puzzled to see that nothing seemed to happen at the distance where αs should noticeably change (or so he thought). The data were completely smooth, with no sign of the blowup he had been led to expect. The measurements didn’t seem to bother more experienced scientists, who were accustomed to collecting data in this region, and there are only so many naive questions that students can ask before exhausting their welcome. So he added this issue to the long list of things that he didn’t understand about the world, to be answered (maybe) later, and moved on.

Jen Christiansen
A few years later he used his data and other measurements from Jefferson Lab to measure a quantity called the Bjorken integral, named after James Bjorken, one of the pioneers of strong force studies. The Bjorken integral has to do with the direction of quark spin inside protons and neutrons, and as a bonus, it also provides a relatively easy way to calculate αs, as long as you stay away from Terra Damnata. So Deur was able to measure αs on the sure-footed domain of short distances. Being curious and inclined to experiment, he also checked what the formula would predict for long distances. This experiment was just for fun, and he knew very well that he wasn’t supposed to take the answer seriously. But his analysis showed that, far from drastically changing as the distance grew, αs stopped growing and became constant.
Deur shared this alarming finding with his Ph.D. mentor, Jian-Ping Chen, a Jefferson Lab staff scientist, who remarked that this αs looked like predictions he’d seen before. Digging into past studies, Deur found other instances of coupling calculations becoming constant at long distances, much like what he saw in his data. Perhaps his playful αs calculation revealed the strong force’s genuine behavior after all? It was a stroke of luck because, although no one had realized it yet, the Bjorken integral is uniquely suited for calculations of αs at long distances. Whereas most measurements probe interactions among many quarks (because quarks are never found alone), the Bjorken integral manages to filter out most of the multiquark processes and separate out effects on individual quarks. It turns out, this calculation of αs would not have worked with almost any other type of nucleon data.
Because Deur’s αs possibly made sense, he wondered whether he could show it at physics conferences without too much risk of ridicule. He worried, though, because his measurements seemed to contradict the prevailing wisdom that the intensity of the strong force would keep growing. But he decided to risk it. As it happened, Brodsky attended one of these conferences and helped Deur put the work on firmer theoretical footing. This meeting was the beginning of a fruitful collaboration that continues to this day.
While Deur was exploring αs experimentally, Brodsky was working with Guy de Téramond Peralta and Hans Günter Dosch to develop a new method to compute QCD properties at long distances. Their strategy uses a mathematical device known as holography (often used to study black holes and gravity) to infer how the strong force behaves with large values of αs in our four-dimensional spacetime (three space dimensions plus one time dimension) using results from calculations for gravity done in five dimensions. (Whether the extra dimension that underlies this method represents actual physics or is simply a mathematical tool to simplify the problem, much like the use of imaginary numbers in classical physics, no one knows.) This novel approach to the physics of the strong force, so-called light-front holography, can determine αs at long distances and predict the interactions that confine quarks and gluons within nucleons.
Brodsky had long been acquainted with αs and knew that attempts to find a unified theory of the electromagnetic, weak and strong forces seemed to require that αs become finite at long range. In fact, he expected such an outcome because quarks are confined within nucleons, which means quark and gluon quantum loops cannot grow larger than the size of the proton. No more loops means no more evolution of the coupling. So although Deur’s measurements of αs did not surprise him, he was delighted to see that it was, in fact, possible to measure αs at long distances and that the result showed constancy.
Brodsky and de Téramond Peralta contacted Deur to discuss how to compute αs using their light-front holography method and went on to calculate it. The result, published in 2010, was gratifying: their αs matched Deur’s experimental data exquisitely. It was all the more remarkable because the calculation had no adjustable parameter. They neither fiddled with settings nor messed with “fudge” factors.
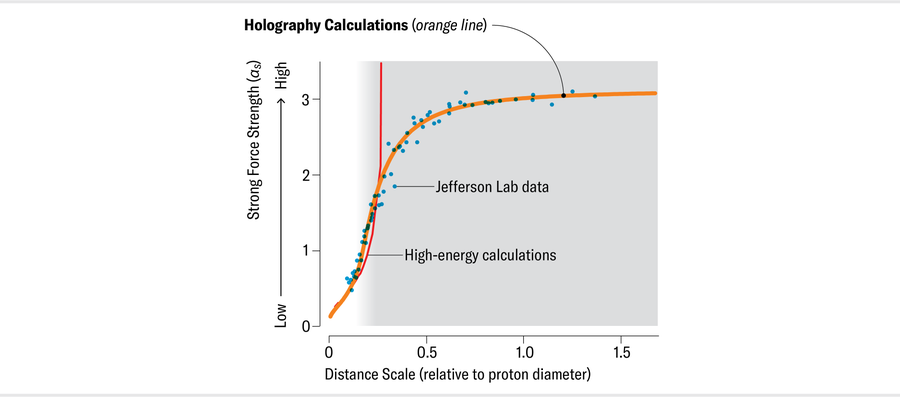
Jen Christiansen
Of course, holography is an exciting, novel approach to quantum chromodynamics (and quantum gravity), but it’s not the same as using QCD itself. But we know that it at least models QCD very well, suggesting future physicists might be able to prove some kind of equivalence between the behavior of gravity and the strong force. Still, to feel comfortable saying we’d truly calculated αs at long distances, we needed a QCD-based computation. A natural approach is to solve the theory’s equations of motion, which in QCD describe how all strong force quantities evolve as spacetime changes.
Deur published his first results on αs in 2005, almost 20 years ago. At the time, Roberts puzzled over them, asking himself what relevance this coupling measurement, seemingly associated exclusively with a single QCD process, could have to the theory’s equations of motion. Such equations need a universal coupling that’s the same for all processes. He put this question aside and moved on.
Nine years later, during a 2014 meeting that he and colleagues organized at the European Center for Theoretical Studies in Nuclear Physics and Related Areas in Trento, Italy, he returned to Deur’s αs. Until this point, theorists had employed two parallel strategies to use QCD’s equations of motion to understand the theory of the strong force. The “top-down” approach tried to predict αs through the properties of gluons. The “bottom-up” approach aimed to use directly measurable quantities to infer αs by comparing predictions with experimental data.
At that 2014 meeting, a prominent colleague pointed out that the two approaches were delivering vastly different results that couldn’t be reconciled. That colleague, however, was unaware of recent progress with the bottom-up approach that Roberts had made with his collaborator Lei Chang. Within 24 hours, spurred by the challenge, the two had results in hand for the bottom-up coupling estimate. They shared them with two leading players in the top-down area who were also at the meeting, Daniele Binosi and Joannis Papavassiliou, and together the group established that the top-down and bottom-up results for αs were mutually compatible. The parallel streams were merged.
Now we were left with a key question: How do we connect Deur’s coupling measurements and the value we compute using QCD’s equations of motion? If we can do that, then we will have bridged the final gap.
Roberts’s next step was to speak with physicist José Rodríguez-Quintero, who had long been working on the top-down approach and had access to results from computer simulations of QCD. After some back-and-forth brainstorming along with Binosi, Papavassiliou and a new team member, Cédric Mezrag, the group arrived at a universal QCD coupling. Amazingly, this result was virtually indistinguishable from both Deur’s data and the holography calculation by Brodsky and his colleagues. Moreover, like the holography result, the new prediction was parameter-free: no nudging or tinkering. That fact meant that the agreement was deeply significant.
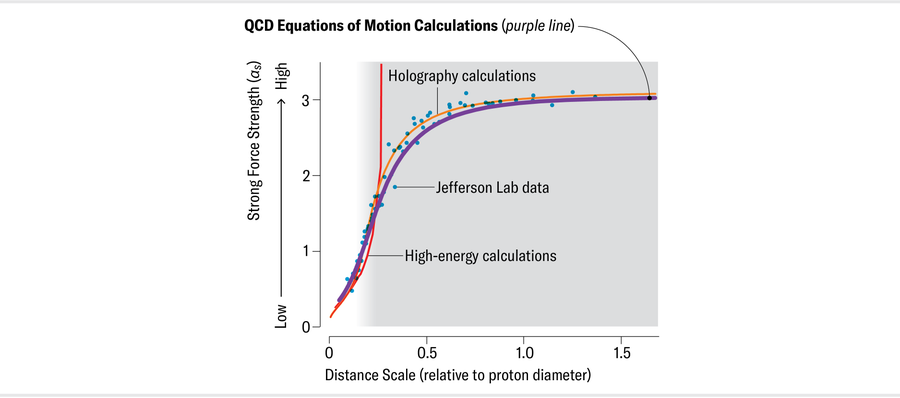
Jen Christiansen
Since that time, capitalizing on improved information from the top-down, bottom-up and simulation approaches, the group has updated its theoretical analysis. The scientists found that, outside Terra Damnata, their coupling and Deur’s data agree to better than 1 percent. Furthermore, moving into Terra Damnata, they discovered that complex interactions between quarks, which could have upset the connection between these couplings, largely cancel out among themselves because of the physical features of the processes underlying the Bjorken integral. This was Deur’s stroke of luck: he had serendipitously chosen the one process whose coupling is most closely related to the universal result derived from QCD’s equations of motion.
Now, for the first time, we have both compelling data and calculations of αs that cover the entire length-scale range, including Terra Damnata, the previously unreachable territory. The key finding is that as the distance grows greater, the coupling stops growing, and the inconstant constant becomes constant once more. This discovery has profound implications.

The CEBAF Large Acceptance Spectrometer took some of the measurements that helped to define the strong force at a scale never possible before.
Courtesy of Jefferson Lab
First, knowing αs at all distances is practically important: physicists can now analytically predict numerous quantities that were previously out of reach. Most phenomena relating to the strong force in nature, from the deepest structure of the atoms within us to the inner workings of neutron stars, are determined by the strength of αs. Because this coupling is dominated by its long-range behavior, which we now know to be finite rather than infinite, we have opened up a new world of possible calculations.
At a deeper level, the solutions of QCD’s equations of motion help to reveal the origin of 99 percent of the visible mass in our universe. This mass comes from atoms, and most of the mass of atoms is in their protons and neutrons (electrons are relatively light). But where does proton and neutron mass come from? The quarks that constitute them also have very little mass of their own. But at the scale of a proton, our revelations about αs suggest that quarks gather clouds of gluons around them that generate much of the mass of the proton. In essence, the powerful binding energy that the strong force exerts to bind quarks together contributes almost all of the mass (remember, Albert Einstein revealed that energy and mass are two sides of the same coin). Therefore, if you weigh 160 pounds, then more than 158 of them come from quantum chromodynamics, specifically because of the mechanism that freezes αs into a constant. The Higgs boson contributes only the small remainder—the tiny mass the quarks and electrons possess on their own.
Even more significantly, the static nature of αs at long distances means that QCD is the first full quantum field theory that predicts only finite quantities. All the other known quantum field theories, including quantum electrodynamics (which describes the electromagnetic force), run into infinite Landau poles at very high energies. As such, QCD may lead the way to explaining many phenomena that lie outside our current understanding.
Pursuing this line of reasoning, we may learn, for example, whether string theories with 10, 11 or 26 dimensions of spacetime are necessary to make sense of our universe or whether, instead, a clear understanding of our solidly established four spacetime dimensions will turn out to be sufficient. The excitement right now among nuclear and particle physicists is tangible.