Henry Ernest Dudeney may be among the most significant puzzle inventors who ever lived. He was born in Mayfield, England, in 1857, the son of a village schoolteacher, and he died in 1930. Dudeney designed brainteasers for newspapers and magazines regularly for decades, and he later compiled most of his puzzles into books. This head-scratcher comes from his 1917 book Amusements in Mathematics.
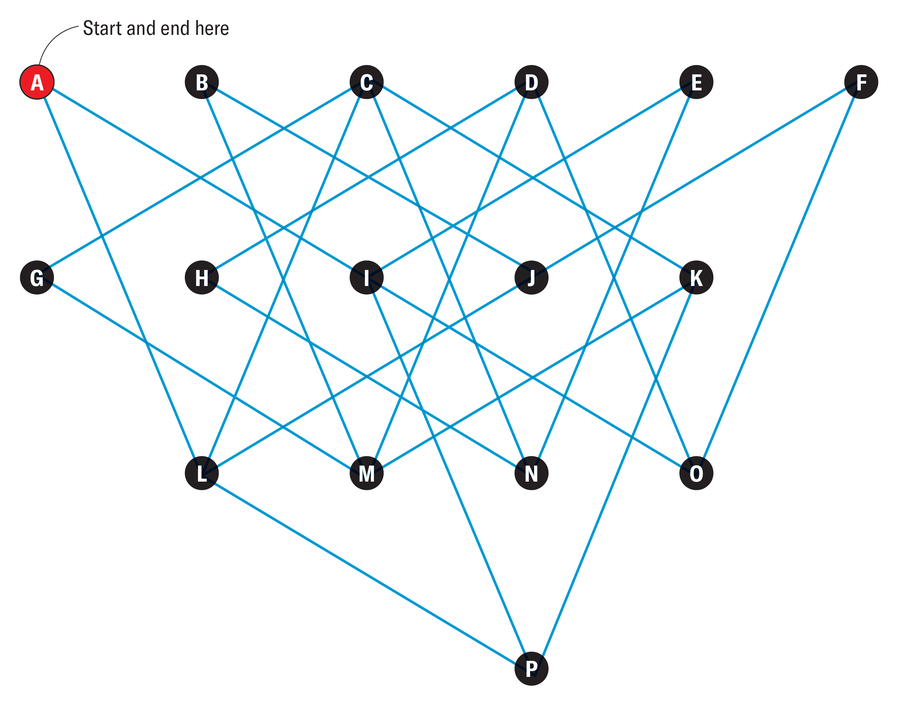
A traveling salesman who lives in city A wants to visit all cities from B to P over the course of a week, though not necessarily in alphabetical order, and return to A at the end. He plans to enter each city exactly once. The blue lines are the only roads connecting the 16 cities. The traveling salesman may use only a straight route between any two cities; he is not allowed to turn at the intersection of two streets. How many different routes are possible?
Answer:
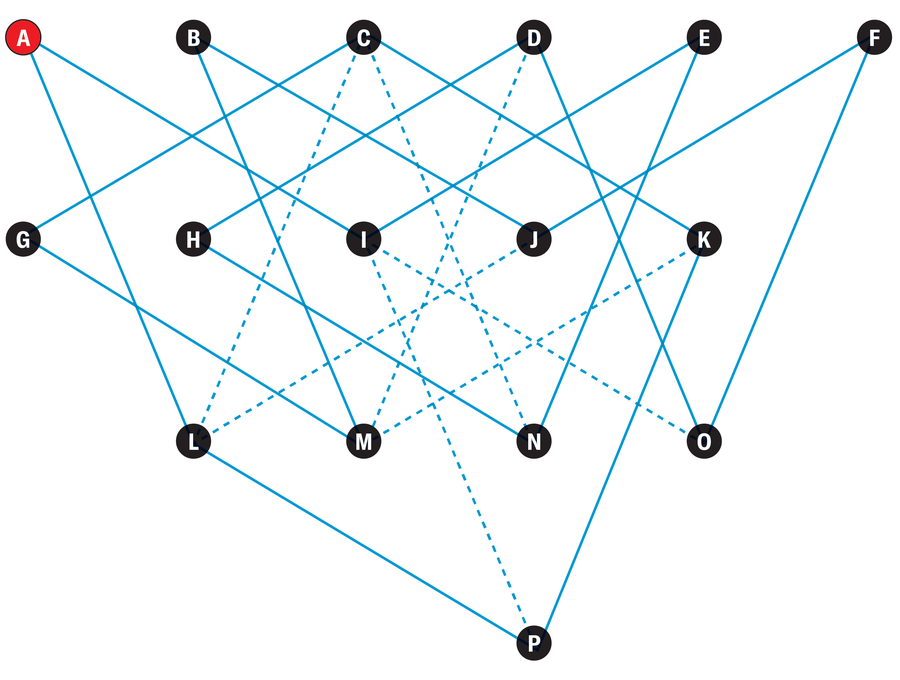
If the traveling salesman enters a city on one road, he must leave it again on another. In order for a round trip to be possible at all, at least two roads must lead to each city. There are exactly two roads leading to cities A, B, E, F, G and H. The traveling salesman must therefore travel on these roads no matter what. This also determines which roads he will use to reach and leave cities I, J, M and N. The remaining connections are then also clear. There is therefore only one possible round trip for the traveling salesman—AIENHDOFJBMGCKPLA—but he can travel it in two different directions.
We’d love to hear from you! E-mail us at games@sciam.com to share your experience.
This puzzle originally appeared in Spektrum der Wissenschaft and was reproduced with permission.