Math Puzzle: An Odd Pyramid

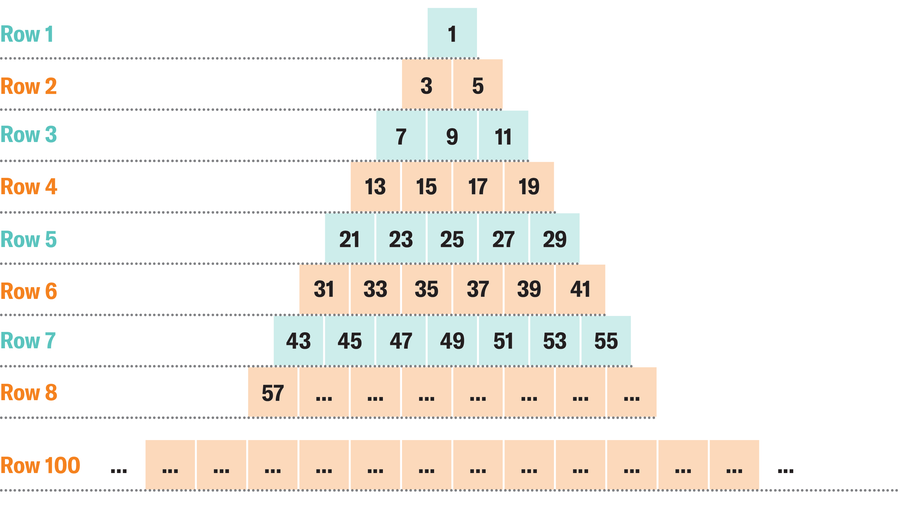
The odd numbers form this pyramid:

What is the sum of the numbers in row 100?

Show puzzle solution

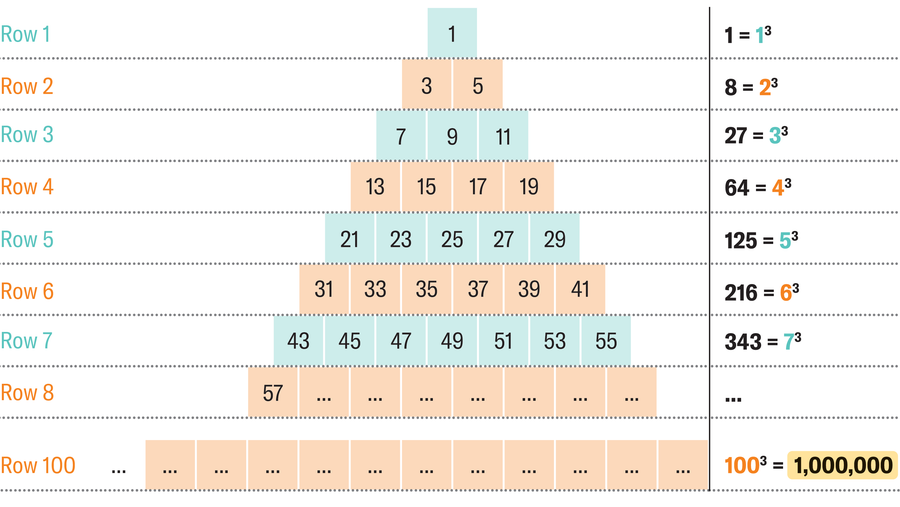
The sum of the 100th row is 100³ = 1,000,000.

If you add up the sum values of rows 1 to 8, the result is always the row number raised to the third power.

For the 100th row, this gives you 100³ = 1,000,000.

This connection can be proven using mathematical induction.

We’d love to hear from you! E-mail us at games@sciam.com to share your experience.

This puzzle originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

Editor’s Note (8/2/24): The solution was edited after posting to correct the translation of mathematical terminology.