In the early 1970s mathematician Donald Knuth spent a sabbatical with his wife in Norway. The time was meant to be spent relaxing. Yet one night he woke up his partner in a state of agitation. He urgently needed to write a book. Don’t worry, he reassured his spouse, it will only take a week. To concentrate on his writing, he reserved a hotel room just for himself in Oslo.
There he drafted what would become Surreal Numbers: How Two Ex-Students Turned On to Pure Mathematics and Found Total Happiness. Though Knuth did not invent the concept of surreal numbers, he was the first to publish a detailed work on the subject and coin the term. To this day, his book is considered the standard work on the subject.
Yet the tome is anything but an ordinary example of nonfiction. It consists of dialogues between two fictional characters, Alice and Bill. It also features the true inventor of surreal numbers, the late mathematician John Horton Conway, who died in 2020.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
“In the beginning, everything was void, and J.H.W.H. Conway began to create numbers,” Knuth wrote. Knuth added extra initials to Conway’s name as an allusion to the Tetragrammaton (the four-letter Hebrew name of God, transliterated as YHWH or Yahweh), he explained in a Numberphile YouTube video.
That’s hardly the only biblical reference; even Knuth’s backstory for writing the book echoes the religious creation story. He put the whole thing to paper in just a week, as he’d promised his wife. “On the sixth day I finished it. On the seventh day I rested,” Knuth told Numberphile.
Surreal numbers are created by adding values between two given preexisting numbers. If you look at 0 and 1, for example, 1/2 is in the middle, 1/4 is between 0 and 1/2, and so on. This approach makes it possible to resolve the number line ever more precisely.
This idea doesn’t sound very spectacular at first, but instead of simply delivering fractions with ever larger denominators, there is a point at which everything explodes, and suddenly values arise that are not even contained in the real numbers.
Two Axioms Result in an Incredible Universe of Numbers
Conway had established two basic rules from which the immeasurable realm of numbers arises. Every number x is defined by two sets, ML and MR, which contain previously created numbers: x = {ML : MR}.
The ML is the left-hand set and MR is a right-hand set. The first rule is that elements of the left-hand set are always smaller than those of the right-hand set.
The second rule states that 0 is the number that is bounded by two empty sets. These two rules lay the foundation for an incredibly diverse branch of mathematics!

A surreal number x results from a value that lies between two sets of numbers ML and MR. Credit: Manon Bischoff/Spektrum der Wissenschaft, restyled by Amanda Montañez
Building on those foundations, Knuth’s creation story for surreal numbers takes place over several days. On the zeroth day, 0 is created out of nothing per the second rule, which he represents as 0 = { : }.
On the first day, two more numbers are created: 1 = {0: } and –1 = { :0}. These two numbers arise because they are the next largest and smallest integers (respectively) on the number line.
The second day of surreal creation gets more interesting. Now you can use different numbers for the first time. For example, {0:1} denotes the number that lies between 0 and 1, that is, 1/2. You can also create {1: } = 2, {–1:0} = –1/2 and { :–1} = –2.
Continue this way and on the third day you get 1/4, 3/4, 3, and so on.
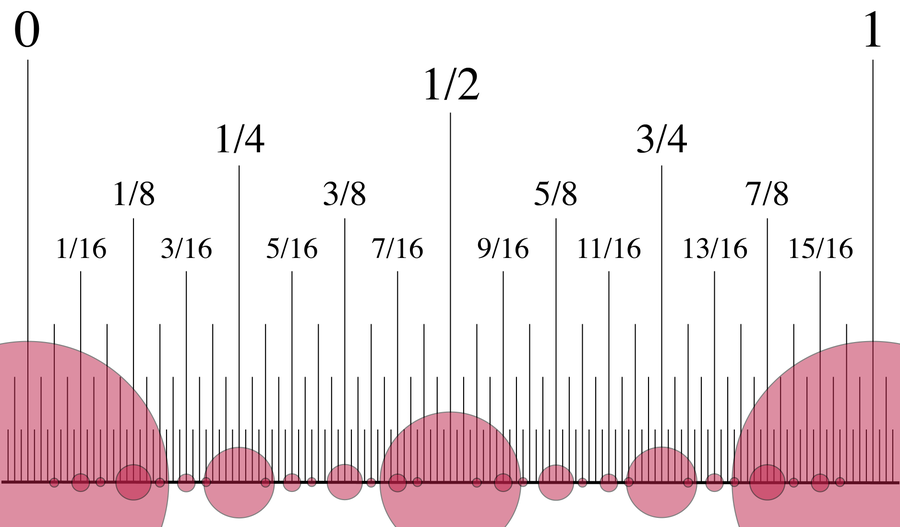
Fractions with multiples of 2 in the denominator emerge gradually in the creation of surreal numbers. Credit: David Eppstein/Wikimedia Commons(CC0 1.0)
If you keep this up, by the nth day, you will have all integers from –n to n and all fractions with denominators 2, 22, 24, 28,... to 2n. Such fractional numbers whose denominator is a multiple of 2 are called dyadic numbers. This makes the surreal numbers seem rather boring: they only consist of integers and dyadic numbers. There is no trace of values such as pi (π) or the square root of two (√2)—nor even a number as trivial as 1/3.
The Dawn of All Real Numbers
The really exciting properties of surreal numbers unfold as soon as you reach the day ω. That omega figure corresponds to a countable infinity. On this day all real numbers that were not there before, that is, all irrational values and all nondyadic fractions, are created in one fell swoop.
For example, √2 results from the following representation: √2 = {1 5/411/8 ... : ... 23/163/2}. Other irrational values such as π are also obtained in this way; the number is enclosed by two dyadic number sequences.
In fact, the procedure is similar to the established Dedekind method, which is used to construct the real numbers from the rational numbers. In that approach two sets of rational numbers are formed, one of which contains smaller numbers than the other (just like Conway’s first rule). The “intersection” between these two sets then defines a real number.
But in Conway’s curious construction, day ω births new numbers. Suddenly, infinite values also arise—namely, the number ω. To do this, you have to insert all natural numbers into the lefthand set and leave the righthand set empty: ω = {1 2 3 ... : }. This corresponds to the number that is greater than all natural numbers.
And there is something even more unusual. If you enter 0 for the left-hand set and all dyadic fractions for the righthand set, you get an infinitesimal number ε = {0 : ...1/81/41/2 1}. This epsilon represents the inverse of infinity: ε is so small that there is no real number that can represent it. And in fact, ε corresponds to the reciprocal of ω: ε = 1/ω. The infinitesimal number ε appears on the day ω not only on its own but also in combination with all integers and dyadic numbers: 1/2 + ε = {1/2 : ... 1/81/41/2 1}.
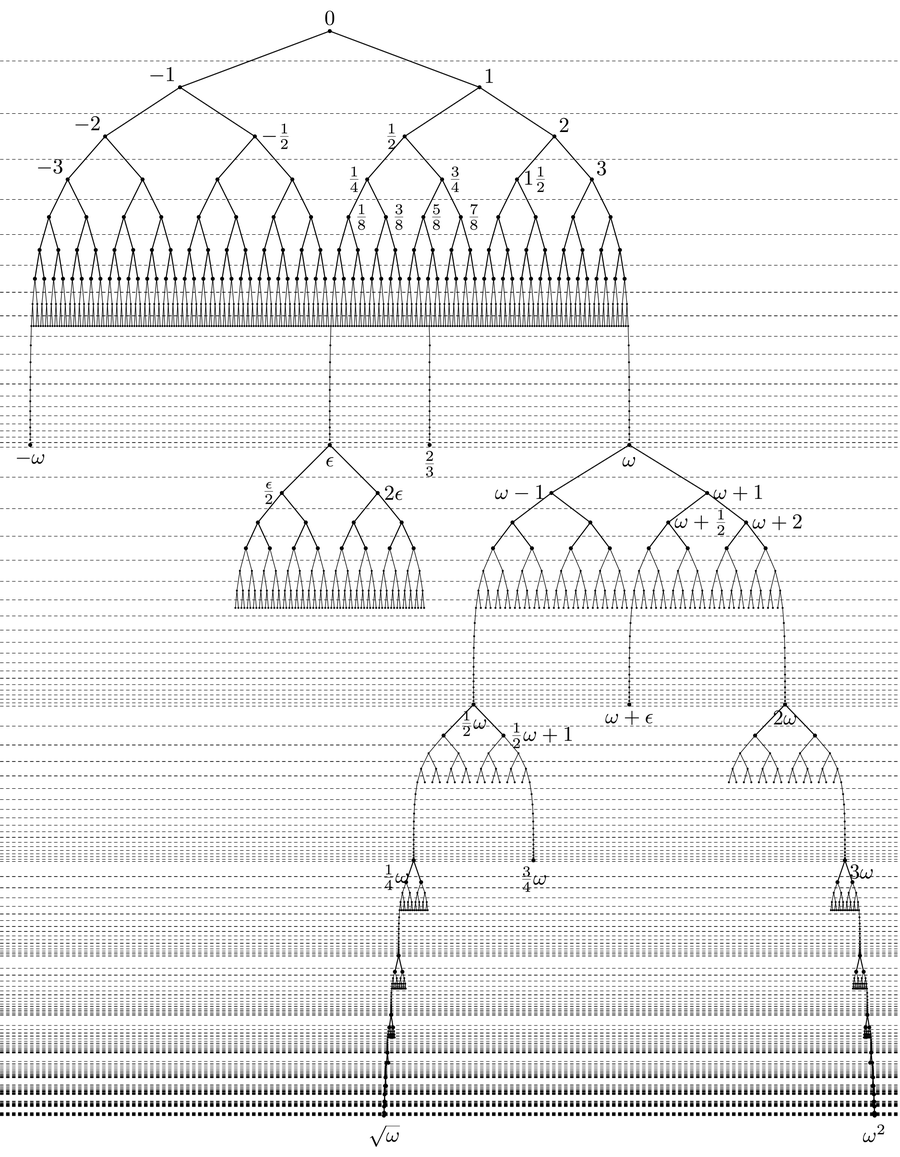
After an infinite number of days, all kinds of numbers are created, from fractions to irrational numbers to infinities and infinitesimals. Credit: Lukáš Lánský/Wikimedia Commons(CC BY-SA 3.0)
On day ω + 1 more surreal numbers arise, such as the numbers ω + 1 and ω – 1, two new infinities. In addition, any real number can now be combined with ε, for example: π + ε = {π : ...1/81/41/2 1}. In addition, the number ε/2 is also created, a value that is half as small as the infinitesimal number.
The Concept of Quantity Collapses
On each subsequent day, new surreal numbers emerge: new infinities and infinitesimals, as well as new values that appear between all the previously generated numbers. Little by little, the variety of numbers continues to grow. In fact, so many objects are created that the surreal numbers can no longer be defined as a set. Instead they form a “class.” As such, they far exceed all other types of numbers: natural, rational and real numbers.
To understand that point, think back to the definition of surreal numbers as the two sets ML and MR, where MLis always the smaller of the two. Assume that the totality of all surreal numbers is a set S. Then you could define a new number x as x = {S : }. This would make x a number that exceeds all values of S—so you would have defined a surreal number that is not contained in S.
This is a contradiction because S contains all surreal numbers by definition. To avoid such paradoxes (which also arise if you want to determine the number of all infinities), mathematicians have introduced the concept of a class. Because S is a class, it cannot be used to construct surreal numbers.
And surreal numbers hold further surprises. Although there are significantly more surreal numbers than real numbers, they do not form a continuum. A number line made up of surreal numbers is full of holes—unlike the real number line, which has no gaps. The reason for these spaces is that there are always smaller infinitesimals that squeeze in between the previously generated surreal numbers.
For example, the open set [0,1) includes all values that are smaller than 1. The number 1 is therefore an “upper bound.” Such a concept is missing for surreal numbers, however. That’s because you can find a surreal number between the set [0,1) and 1, such as 1 – ε. This number belongs to neither [0,1) nor 1.

Unlike the real number line, the surreal number line includes gaps where smaller infinitesimals fit. Credit: Manon Bischoff/Spektrum der Wissenschaft, restyled by Amanda Montañez
This observation has far-reaching consequences. It means that a sequence of numbers such as 1/n does not have a limit value of 0 if n approaches infinity. Instead the sequence does not converge. It continues to run for all eternity while it takes on the ever smaller values ε, ε/2, ..., ε/100, and so on. In the universe of surreal numbers, 0.9999... can never equal 1—unlike with real numbers.
With such missing limits, the usual form of analysis that we learn at school in the form of derivatives and integrals also collapses. All fundamental concepts are based on limit value formation and a continuous number space. Nevertheless, experts have succeeded in developing what is called a “nonstandard analysis,” which works with surreal numbers.
Even if it all seems very abstract and strange, Knuth is convinced that surreal numbers are just as suitable for describing our world as any other. If “everybody for a hundred years had learned about this in school, [they would have] considered that this is the way numbers are,” he told Numberphile. “There is no reason for us to think that the universe obeys the laws of real numbers.” In fact, physicists have already tried to incorporate surreal numbers into their theories. The effort involved is usually very high, however, and the benefits have so far been marginal.
In mathematics surreal numbers form an interesting structure: an enormous number system that can be used to describe both infinities and infinitesimals. Conway actually came up with this astonishing construction when he was investigating the strategies of the game Go. Surreal numbers have proven themselves in game theory but only in their finite variant as a union of integers and dyadic numbers. As Conway reflected in a lecture in 2016, the fact that he revealed the infinite expanse of a previously unknown universe of surreal numbers in this way was “the biggest surprise of [his] mathematical life.”
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.
